El árbol binomial multiperiodo parte del precio actual del subyacente, So, valiéndose de unos parámetros de revalorización del precio, o up, y dedepreciación del precio, o down, con las que se forman las distintas trayectorias o caminos que puede seguir el precio de una acción, o cualquier otro subyacente, Su y Sd. Cada una de estas trayectorias tiene asociada una probabilidad denotada como p y 1-p, respectivamente. Con el fin de conseguir una mayor apreciación de la construcción de un árbol binomial multiperiodo, se muestra la forma del mismo para dos instantes de tiempo:
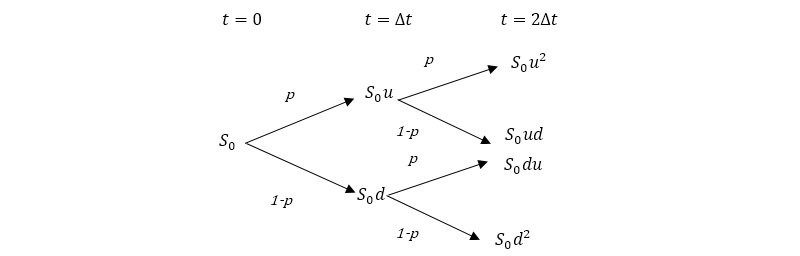
Siguiendo con el modelo propuesto por John C. Cox, Stephen A. Ross y Mark Rubinstein en 1979 (en adelante CRR), presentan como resultado final las siguientes formulaciones de cada uno de los parámetros. Nótese que el modelo fundamenta en el Método de Duplicación de Carteras basado en la construcción de una cartera híbrida compuesta por acciones y bonos, donde se eliminan las oportunidades de arbitraje y se parte de la premisa de neutralidad al riesgo.
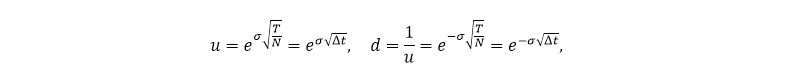
siendo T=NΔt la fecha del vencimiento y N el número de períodos del árbol de longitud Δt. Obsérvese que queda garantizado que dup en el precio del subyacente (p) y aquella asociada a la trayectoria down (1-p):
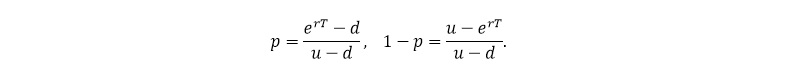
Respecto al parámetro r, este representa la tasa de interés libre de riesgo, lo que implica asumir que el rendimiento esperado de la acción equivale a dicho tipo de interés, en coherencia con la hipótesis fundamental de estas metodologías, el principio de neutralidad al riesgo.
Supone un gran error de interpretación del modelo considerar de forma individual las trayectorias del árbol en cada periodo. La comprensión correcta del mismo reside en el cálculo del promedio en cada uno de los instantes de tiempo en los que se realiza la estimación de precios, en función de las probabilidades de las ramas intermedias del árbol, es decir, de los nodos intermedios, en este caso, denotados como Qtj:
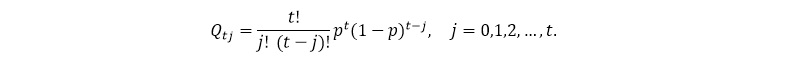
Una vez estimado el precio del subyacente para cada instante de tiempo (recuérdese, como un promedio de las probabilidades de los nodos intermedios por el precio obtenido en cada una de las trayectorias) resulta ineludible realizar la validación del modelo. Para ello, se han seleccionado 22 precios diarios de cierre ajustado de una acción cotizada del IBEX 35 durante el pasado mes agosto del año en curso, con el fin de estimar su precio de cierre durante el mes de septiembre, es decir, 22 periodos a estimar. Previamente se han calculado los parámetros del modelo, p, u y d, por simplificación se ha asumido una hipotética tasa de interés libre de riesgo diaria. Para finalizar con la aplicación del modelo, en este caso, se han seleccionado como medidas de bondad de ajuste el Error Porcentual Absoluto Medio, más conocido como MAPE y la construcción de Intervalos de Confianza. A continuación, se muestra los resultados de la aplicación del modelo.
· Precio de cierre ajustado de una acción cotizada e incluida en el IBEX-35:
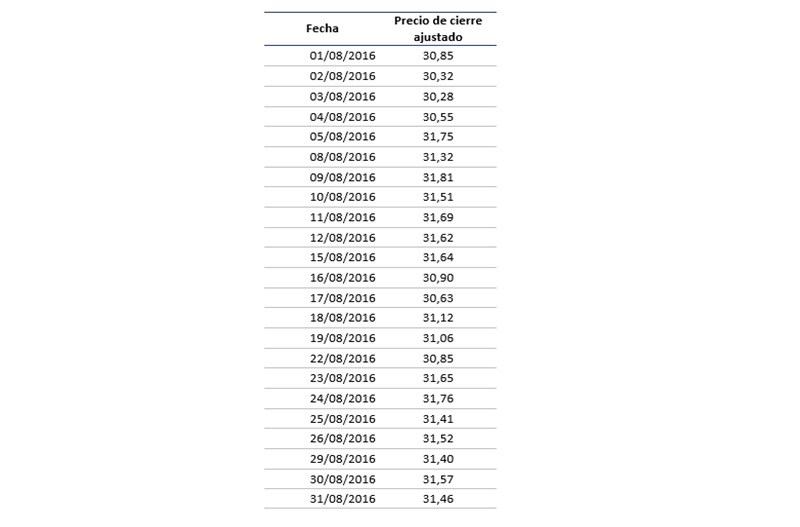
· Parámetros del modelo CRR:

· Gráfico comparativo del precio observado, estimado e ilustración del Intervalo de Confianza (para más detalle sobre la construcción del árbol binomial véase Anexo):
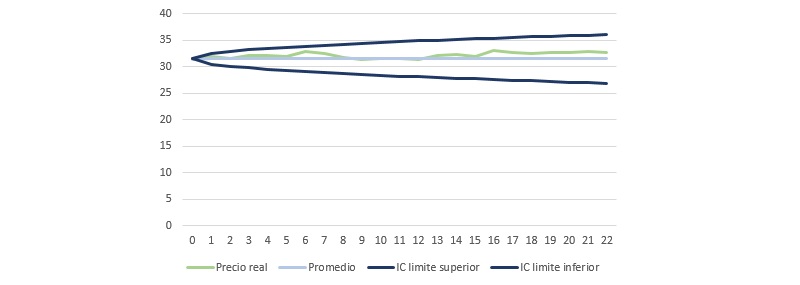
Los resultados de la aplicación del modelo arrojan un ajuste notablemente preciso. Por el lado del MAPE, este ha resultado menor del 5%, nivel máximo de error tolerable que suele considerar en este tipo de modelos. Asimismo, el gráfico muestra una gran bondad de ajuste, sobre todo, entre los periodos 9 a 12 donde la estimación coincide prácticamente con el precio real del subyacente, de hecho, el gráfico obtenido tiene un comportamiento muy parecido al que se obtendría mediante un modelo log-normal. Si bien, sería un gran error no tener en cuenta la esencia base del modelo, que puede llevar a errores en su interpretación o incluso una posible idealización del mismo, dado los resultados obtenidos. Las hipótesis seguidas por el modelo se alejan de la realidad del mercado financiero actual, sobre todo en lo que respecta al principio de neutralidad del riesgo, dado que un inversor siempre exigirá mayor rentabilidad en función del riesgo que asuma por la operación. Asimismo, el modelo presenta buenos resultados cuando la volatilidad de los rendimientos del subyacente es pequeña, por lo que dependerá del analista la selección correcta del modelo a implementar para la valoración.
Natalia Mariz Avis

